この記事は Stan Advent Calendar 2016 のエントリーです。
Stanいいですね。いいですね,Stan.
私はもっぱらRから触るrstanユーザーなんですが,いろいろなところから触れる間口の広さがいいですね。
もちろん「尤度関数を書かなくても推定してくれる」とか「細かい設定をしなくても大体ちゃんとやってくれる」といったStan本来のありがたみも忘れちゃいけません。
なにより,ベイジアンモデリングのハードルがすごく下がった気がします。頭の中でイメージしていることが,そのまま書けるっていうのは,とてもいいことだと思うのです。
この「頭の中のイメージがそのまま書ける」ということを一番実感したのは,状態空間モデルのお勉強をしているときでした。なので,その時のことを記事にして,Stanへの感謝とエールに代えたいと思います。
時系列データと状態空間モデル
時系列的なデータの場合,一つ前の時点との関係(自己相関)が強いもんだから,そのままの分析じゃダメで,時系列分析という別の考え方が必要になる。これはまあいいです。
でも,従来の(最小自乗法,最尤推定法的な)時系列分析はなんだかわかりにくい。
時系列分析については,いろいろな本も出ています。あるいはこちらのサイトはすごく丁寧にわかりやすく書いてくれていますので,時間かけて読めば何をやっているかはちゃんとわかります。でも,ちゃんと面倒なことがわかります。
というのも,とある時点での推定値がでても,それが期間全体で成立するかどうかを前後にわたってチマチマ調整していかなければならないからです。私の理解したイメージでは,基本的にt時点からt+1時点への回帰で,それがワンステップ前,ワンステップ後でも推定地として大丈夫かどうか,均してからつかうという感じ。すごい力技な感じがするんですね。実際,モデルを決める,パラメタを求めて,フィルタをかけて,スムージング,という順番でやらないといけないのです。
そこで出ました状態空間モデル。これは
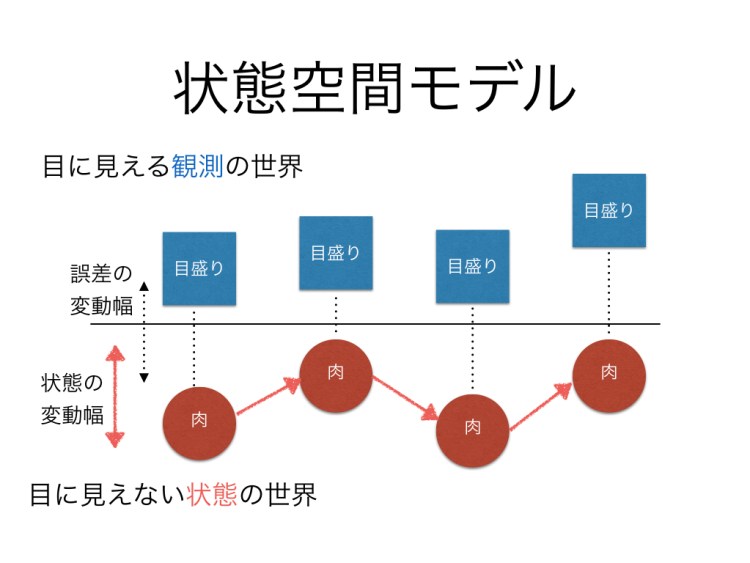
- 目に見える観測の世界
- 目に見えない状態の世界
を区別して,状態は連綿と続いていく,観測はそれに誤差が乗っかる,というイメージでモデリングしていくのですが(これについてもこちらのサイトが詳しいです!),Stanはこのイメージをモデルに書くときに,本当にそのまんま!という感じなのです。これを実際の例で見ていきましょう。
状態空間モデルによる体重の予測
私はなぜか,毎朝起きたら体重と体脂肪を測定して記録する,というのを日課にするようになっているのですが,この習慣が2012年ごろから続いており,時折記録できない日(出張で自宅にいない=いつもの体重計がない場合)なんかもありつつ,2016年7月末の段階で1077レコードありました。
実は昨年末帰省したときに,京都ラーメンが美味しすぎてたくさん食べていたら,体重が最高83kgまで達しまして,これはまずいんじゃないか(当方身長173cm)と,今年に入ってから少し体重を下げる努力をしております。この辺の効果なんかも考えてみたいところです。
さて,状態空間モデルは「観測値」と「状態」を区別すると言いました。ここでは,観測値=体重計の目盛りです。でもうちの体重計は,結構数字を出すのに悩むんですね。77.4?77.5?77.3?いやまて77.7・・・?とか考えてから,今日は77.6kgです,と表示したり。体の傾け方とかで数値がぶれるのかしら,と思うのですが,まあこの目盛りは信じるしかない。
こうした測定誤差とは別に,肉がついてるとか落ちたとかいう実際の状態もあるわけで,そこを別なものとしてモデリングします。下のイメージ図参照。
さて,これをStanでかくと,モデルの部分はまさにこのイメージのまま,なのです。
data {
int n; # サンプルサイズ
vector[n] W; # 体重データ
}
parameters {
real muZero; # 左端
vector[n] mu; # 確率的レベル
real<lower=0> sdV; # 観測誤差の大きさ
real<lower=0> sdW; # 過程誤差の大きさ
}
model {
# 状態方程式の部分
# 左端から初年度の状態を推定する
mu[1] ~ normal(muZero, sdW);
# 観測方程式の部分
for(i in 1:n) {
W[i] ~ normal(mu[i], sdV);
}
# 状態の遷移
for(i in 2:n){
mu[i] ~ normal(mu[i-1], sdW);
}
sdV ~ cauchy(0,5);
sdW ~ cauchy(0,5);
}
いかがでしょうか。観測データ(W[n])は実際の肉(mu[i])に誤差(sdV)がついて変化します。実際の肉(mu[i])は昨日の肉(mu[i-1])に誤差(sdW)がついた形で変化します。
モデルのイメージ図をそのまま書いただけになっているのです!フィルタとかスムージングとかいりません!
欠測と予測
自宅の体重計で毎朝測るのですが,自宅で目覚めない日もあるわけで,そういう日は測定できません。欠損値になります。
それでも肉がなくなるわけではないので,状態は続いていきます。これをモデリングする場合は,測れなかった日の観測値もパラメータとして推定してやれば良いのです。
Stanは残念ながら欠測値に対応していませんから,「これは欠損だよ」「観測データはちゃんと揃ってるよ」という形で渡してあげなければなりません。私はここで,欠測のところに特殊な数字(9999)を入れて,Stanに渡してあげることにしました。
W <- dat$weight #データの体重部分 Nmiss <- sum(is.na(W)) #欠測値の数を数えます W <- ifelse(is.na(W),9999,W) #データがもし欠損であれば9999という数字を入れろ,としてあります。 datastan <- list(n=length(W),W=W,Nmiss=Nmiss)
ついでに。
時系列的な変化は,やはり未来に向けての予測がしたいですよね。予測,というのも「(まだ)観測されていないデータ」という意味で,欠損値ですから,同じアルゴリズムが使えます。

予測したい日数を欠損としてデータセットに加えてやれば,この問題は解決です。先ほどのコードにちょいと付け足します。
W <- dat$weight #データの体重部分 Nmiss <- sum(is.na(W)) #欠測値の数を数えます predN <- 200 # データの後200日分予測して見ましょう(やりすぎ) Nmiss <- Nmiss + predN #欠損値の数が増えます W <- ifelse(is.na(W),9999,W) #データがもし欠損であれば9999という数字を入れろ,としてあります。 predW <- rep(9999,predN) # 予測の分もデータにします W <- c(W,predW) #元のデータに追加 datastan <- list(n=length(W),W=W,Nmiss=Nmiss)
これでよし。さて,Stanのコードはどうなっているかというと,
data {
int<lower=0> n; # データ総数
vector[n] W; # 体重データ
int<lower=0> Nmiss; # 欠損値の数
}
parameters {
real muZero; # 左端
vector[n] mu; # 確率的レベル
vector<lower=0>[Nmiss] Miss_W;欠測値はパラメータ
real<lower=0> sdV; # 観測誤差の大きさ
real<lower=0> sdW; # 過程誤差の大きさ
}
model {
# 状態方程式の部分
# 左端から初年度の状態を推定する
mu[1] ~ normal(muZero, sdW);
# 観測方程式の部分
{
int nmiss;
nmiss = 0;
for(i in 1:n) {
if(W[i]!=9999){
W[i] ~ normal(mu[i], sdV);
}else{
nmiss = nmiss+1;
Miss_W[nmiss] ~ normal(mu[i],sdV);
}
}
}
# 状態の遷移
for(i in 2:n){
mu[i] ~ normal(mu[i-1], sdW);
}
sdV ~ cauchy(0,5);
sdW ~ cauchy(0,5);
}
観測方程式のところに,missを埋めていくインデックス,nmissというのを作りました。これは0からカウントしていきます。
もし観測(w[i])が9999じゃなかったら,それまでどおり肉の状態(mu[i])に誤差がついた形であらわれているのですが,もし9999だったら=欠測だったら,肉の状態(mu[i])からでてきた推測すべきパラメータ(Miss_W)になるよ,ということです。
そして欠測していようがしていまいが,肉の状態は1-step前の状態から推移し続けます。
これで推定してみた結果は次の通り。
Inference for Stan model: Missing and Predict.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
sdV 0.38 0 0.03 0.32 0.36 0.38 0.4 0.44 297 1.02
sdW 0.18 0 0.03 0.13 0.16 0.18 0.2 0.25 111 1.04
Samples were drawn using NUTS(diag_e) at Fri Nov 11 11:03:54 2016.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
上が観測の誤差成分,下が状態の誤差成分です。観測成分による誤差が状態の誤差の約2倍ぐらいあります。
実際のお肉の状態は次のような感じ。
Inference for Stan model: Missing and Predict.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu[1] 81.85 0.01 0.45 80.96 81.56 81.86 82.15 82.73 1415 1.00
mu[2] 81.85 0.01 0.41 81.04 81.58 81.86 82.13 82.63 1274 1.00
mu[3] 81.86 0.01 0.36 81.17 81.61 81.86 82.10 82.56 1267 1.00
mu[4] 81.86 0.01 0.30 81.27 81.66 81.86 82.05 82.45 1223 1.00
mu[5] 81.86 0.01 0.23 81.41 81.70 81.86 82.02 82.30 1039 1.00
(以下略)
ほうほう・・・。
さて,この記事は事前に描いて今日公開するよう予約投稿してあるのですが,今年のお正月から7月末までの前半期をつかって,この12月1日の体重を予測しますと!
> dat[338,]
date mu LowerMu UpperMu estW
NA.105 2016-12-01 74.19501 69.86548 78.03625 74.20741
実は74.1950kgなお肉の状態になっているはずです!当たってるかい?今日の俺よ。
まあ95%確信区間でいくと69.86-78.03kgの間に入って入ればStanの勝ちということです!
確信区間も含めて推移をグラフにしてみると,測定が終わった次の日からパッと幅が広がっていくのがよく見えます。そりゃそうだよねー。
ともあれ,いわゆる時系列分析をするよりも,Stanでもベイジアンモデリングしたほうが直感的にわかりやすいし,簡単だと思うので,超オススメです。
もちろんこの「状態」のところに,予測するモデルを入れていって,より複雑なモデリングにすることができます。私は曜日によって違うんじゃないかとか,出張の前後で体重が変わるんじゃないかとか,いろいろ細かな変数を入れて推測させて見ましたが,ほとんど効果がなかったので,ここではそうしたモデリングの部分はご紹介しませんでしたが。
さあEnjoy Stan!


3件のコメント
コメントは受け付けていません。